움직 도르래를 수학적으로 이해하기

일의 원리를 설명할 때 반드시 빠지지 않고 나오는 것 중의 하나가 도르래이다. 그 중에서도 움직 도르래의 경우 힘의 분산을 통해서 일의 원리를 설명한다. 다시 말해서, 힘이 분산으로 물체에 작용하는 힘의 크기가 물체 무게의 반으로 줄고, 대신에 줄을 당기는 길이가 물체의 올라간 높이보다 두 배가 되므로 직접하는 일이나 움직 도르래로 하는 일이나 같다는 것이다.

결국, 줄을 당기는 길이를 경험적으로 증명하거나, 또는 역으로 일의 원리를 바탕으로 줄을 당기는 길이가 두 배가 된다는 것을 증명한다. 이것은 물리적 관점에서 이해한 것이다. 그렇다면, 일의 원리나 힘의 분산에 의존하지 않고 줄을 당기는 길이가 물체 이동 거리의 두 배가 된다는 것을 증명하는 방법은 없을까 ?

지금부터 그 방법을 알아보자. 다음은 움직 도르래로 물체를 들어올리고 있는 그림이다.

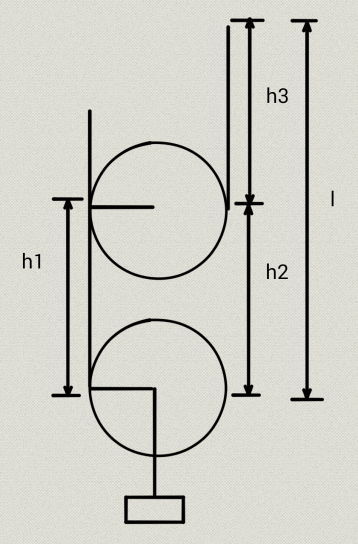
증명을 간단히 하기 위해서 아래쪽 도르래 중심의 오른쪽에 줄의 끝이 닿아 있다고 하자. 이제 물체를 h1 만큼 들어올린다. 이렇게 되면 위쪽 도르래 중심과 아래쪽 도르래 중심의 차이는 h1 이 된다. 이때 h1 = h2 이다. 그렇다면 h3, 곧 물체를 들어올릴 때 감긴 줄의 길이는 얼마가 될까 ?

먼저 물체를 들어올리기 전의 걸려 있는 줄의 길이를 계산해 보자. 위쪽 도르래 중심의 왼쪽에 닿아있는 부분부터  아래쪽 도르래 중심의 왼쪽까지 걸려 있는 줄의 길이는 h1 이다. 그리고 나머지 줄의 길이는 도르래 둘레의 절반이다.

이번에는 물체를 들어올리고 나서 걸려 있는 줄의 길이를 계산해 보자. 위쪽 도르래 중심의 왼쪽에서부터 도르래를 걸쳐 오른쪽 위로 있는 줄의 길이를 계산하면 된다. 도르래에 걸쳐 있는 줄의 길이는 도르래 둘레의 절반이고, 올라가 있는 줄의 길이는 h3 이다. 이 때, 위쪽 도르래 중심 왼쪽에서부터 줄 끝까지의 길이는 같아야 한다. 따라서

h1 + 도르래 둘레 절반 = 도르래 둘레 절반 + h3

가 성립하고, 결국 h1 = h3 가 된다.

이제 줄의 이동 거리 l 을 계산할 수 있다.

l = h2 + h3

이고, h1 = h2 = h3 이므로

l = 2h

가 된다. 따라서 줄의 이동 거리는 물체 이동 거리의 두 배가 된다.

이로써 일의 원리나 힘의 분산 같은 물리적 원리에 의존하지 않고, 간단한 수학적 방법으로 움직 도르래에서 줄의 이동 거리는 물체 이동 거리의 두 배가 됨을 증명했다.