위치 에너지와 운동에너지 공식 유도
에너지는 일을 할 수 있는 능력을 뜻한다. 그리고 외부에서 어떤 물체에 일을 해주면, 그 물체의 에너지는 증가하고, 거꾸로 그 물체가 외부에 일을 해주면 그 물체의 에너지는 감소한다. 다시말해서, 일과 에너지는 서로 전환될 수 있는 것이다. 실제로 일과 에너지의 단위는 같다.
이를 바탕으로 위치 에너지와 운동 에너지의 공식을 유도해보자.
위치 에너지는 어떤 물체가 기준면으로부터 어떤 높이에 위치해 있을 그 물체가 가지는 에너지를 뜻한다. 이 위치 에너지의 공식은 다음과 같다.
앞에서도 말했듯이 외부에서 일을 한만큼 물체의 에너지는 증가한다. 따라서 위치 에너지의 크기는 그 물체를 기준면으로부터 해당 높이까지 들어올리는데 한 일의 크기와 같다. 물체를 들어올릴 때 한 일은 다음과 같다.
물체의 들어올릴 때 필요한 힘은 물체의 무게와 같고, 이동거리는 물체의 높이와 같으므로,
그리고 한 일의 크기는 곧 증가한 에너지의 크기이므로,
운동 에너지는 움직이고 있는 물체가 가지고 있는 에너지를 뜻한다. 이 운동 에너지의 공식은 다음과 같다.
운동 에너지는 곧 그 물체가 정지 상태에서 해당 속력을 가질 때까지 물체에 해 준 일과 같으므로, 물체에 해 준 일을 계산하면 물체의 운동 에너지를 계산할 수 있다.
여기에서 힘의 크기 F 가 일정하다고 가정하면 등가속도 운동이 되므로,
그런데 정지 상태에서 출발했으므로 처음 속력 v0 는 0 이다. 이를 정리하면
그런데, 가속도의 정의를 이용해서 식 (1)을 이렇게 전개할 수도 있다.
처음 속력과 처음 시각은 0 이므로,
하지만, 여기에서 자칫 실수하면 엉뚱한 결과를 얻게 되는데, 속력 = 거리 / 시간 를 이용할 때이다.
이런 결과가 나오는 것은 서로 다른 속력을 같은 문자 v 로 나타내기 때문이다. 처음에 쓰인 v 는 나중 속력을 나타내는 순간 속력이지만, 나중에 거리 / 시간 을 통해 얻은 v 는 전체 이동 구간에 대한 평균 속력이다. 등가속도 운동일 때 전체 구간의 평균 속력은 처음 속력과 나중속력을 더한 후 2 로 나눈값이다. 따라서 이 경우에 평균속력은 나중 속력의 절반이 된다. 결국 위 식은 이렇게 써야 한다.
이를 바탕으로 위치 에너지와 운동 에너지의 공식을 유도해보자.
위치 에너지
위치 에너지는 어떤 물체가 기준면으로부터 어떤 높이에 위치해 있을 그 물체가 가지는 에너지를 뜻한다. 이 위치 에너지의 공식은 다음과 같다.
(Ep : 위치 에너지, m : 물체의 질량, g : 중력가속도, h : 기준면으로부터의 높이)
앞에서도 말했듯이 외부에서 일을 한만큼 물체의 에너지는 증가한다. 따라서 위치 에너지의 크기는 그 물체를 기준면으로부터 해당 높이까지 들어올리는데 한 일의 크기와 같다. 물체를 들어올릴 때 한 일은 다음과 같다.
(W : 한 일, F : 힘의 크기, s : 이동 거리)
물체의 들어올릴 때 필요한 힘은 물체의 무게와 같고, 이동거리는 물체의 높이와 같으므로,
그리고 한 일의 크기는 곧 증가한 에너지의 크기이므로,
운동 에너지
운동 에너지는 움직이고 있는 물체가 가지고 있는 에너지를 뜻한다. 이 운동 에너지의 공식은 다음과 같다.
(Ek : 운동 에너지, m : 물체의 질량, v : 물체의 속력)
운동 에너지는 곧 그 물체가 정지 상태에서 해당 속력을 가질 때까지 물체에 해 준 일과 같으므로, 물체에 해 준 일을 계산하면 물체의 운동 에너지를 계산할 수 있다.
(W : 한 일, F : 힘의 크기, s : 이동 거리, m : 질량, a : 가속도)
여기에서 힘의 크기 F 가 일정하다고 가정하면 등가속도 운동이 되므로,
(v : 나중 속력, v0 : 처음 속력)
그런데 정지 상태에서 출발했으므로 처음 속력 v0 는 0 이다. 이를 정리하면
그런데, 가속도의 정의를 이용해서 식 (1)을 이렇게 전개할 수도 있다.
처음 속력과 처음 시각은 0 이므로,
하지만, 여기에서 자칫 실수하면 엉뚱한 결과를 얻게 되는데, 속력 = 거리 / 시간 를 이용할 때이다.
이런 결과가 나오는 것은 서로 다른 속력을 같은 문자 v 로 나타내기 때문이다. 처음에 쓰인 v 는 나중 속력을 나타내는 순간 속력이지만, 나중에 거리 / 시간 을 통해 얻은 v 는 전체 이동 구간에 대한 평균 속력이다. 등가속도 운동일 때 전체 구간의 평균 속력은 처음 속력과 나중속력을 더한 후 2 로 나눈값이다. 따라서 이 경우에 평균속력은 나중 속력의 절반이 된다. 결국 위 식은 이렇게 써야 한다.
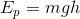










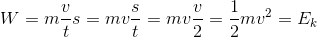

댓글
댓글 쓰기